Stokes Law Equations Formulas Calculator - Terminal Fall Settling Velocity

Fluid Mechanics Hydraulics

Problem:

Solve for fall, settling or terminal velocity.

Enter Calculator Inputs:

acceleration of gravity (g)

particle diameter (d)

density of particle (ρ_p)

density of medium (ρ_m)

viscosity of medium (μ)

Can you share this page? Because, it could help others.

Solution:

Enter input values and press Calculate.

Solution In Other Units:

Enter input values and press Calculate.

Input Unit Conversions:

Enter input values and press Calculate.

Change Equation or Formulas:

Tap or click to solve for a different unknown or equation

	terminal, fall or settling velocity
	acceleration of gravity
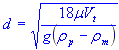	particle diameter
	density of medium (e.g. water, air, oil)
	particle density
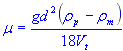	viscosity of medium

References - Books:

P. Aarne Vesilind, J. Jeffrey Peirce and Ruth F. Weiner. 1994. Environmental Engineering. Butterworth Heinemann. 3rd ed.

Background

Terminal velocity is a fascinating concept in various scientific and engineering fields. It is the maximum velocity a falling object reaches when the resistance of the medium through which it falls prevents further acceleration. Understanding how to calculate terminal velocity is vital for engineers, physicists, and environmental scientists. This detailed guide will elaborate on solving for terminal velocity (V_t) using Stokes' Law, tailored for spherical particles moving through a viscous fluid.

Terminal velocity is crucial in fluid dynamics and applies under conditions where objects reach a constant speed due to the balancing forces of gravity and drag. Stokes' Law provides a way to calculate the terminal velocity of a spherical particle moving through a viscous medium, assuming laminar flow and neglecting buoyancy effects.

Equation

For a sphere in motion through a viscous fluid, based on Stokes' Law, the terminal velocity (V_t) can be calculated using the formula:

V_t = 2gd² (ρ_p - ρ_m) / 18μ

Where:

V_t - terminal velocity
g - gravitational acceleration
d - diameter of the particle
ρ_p - density of the particle
ρ_m - density of the medium
μ - dynamic viscosity of the medium

How to Solve

Identify all the given quantities:

Ensure you have the values for the particle's diameter (d), the densities of the particle (ρ_p) and the medium (ρ_m), the acceleration due to gravity (g), and the viscosity of the medium (μ).

Substitute the values into the equation:

Replace the placeholders in the Stokes' Law equation with your specific values.

Solve for (V_t):

Perform the necessary calculations following basic algebraic rules to solve for the terminal velocity.

Example

Calculate the terminal velocity of a spherical pollen grain (density = 1,400 kg/m³) with a diameter of 0.0002 m in air (density = 1.2 kg/m³, viscosity = 1.8 x 10^-5 Pa·s) given g = 9.81 m/s².

V_t = 2 * 9.81 * (0.0002)² * (1400 - 1.2) / (18 * 1.8 * 10^-5)

V_t = 2 * 9.81 * 4 * 10^-8 * 1398.8 / (18 * 1.8 * 10^-5)

V_t = 0.0110748416 / (3.24 * 10^-4)

V_t = 0.034 m/s

Fields/Degrees It Is Used In

Aerospace Engineering: Designing parachutes and understanding the dynamics of objects re-entering the Earth's atmosphere.
Biomedical Engineering: Studying blood flow dynamics and the behavior of microorganisms or particles within bodily fluids.
Environmental Science: Estimating the settling velocities of particulate matter in air or water for pollution modeling.
Mechanical Engineering: Analyzing the behavior of suspended particles in lubricants and other fluids.
Meteorology: Understanding raindrops' fall rates and aerosols' dispersion in the atmosphere.

Real-Life Applications

Air Filtration Systems: Designing filters that effectively capture particles based on their terminal velocities.
Sedimentation Processes: In water treatment, to remove suspended particles by allowing them to settle.
Forensic Science: Analyzing patterns of blood droplet falls in crime scene investigations.
Pollution Control: Modeling the dispersion and settling of industrial pollutants in the air or water bodies.
Sports Science: Understanding the dynamics of balls or objects in motion, considering air resistance.

Common Mistakes

Ignoring the Importance of Units: Always convert all measurements to the SI unit system before calculations.
Neglecting the Laminar Flow Condition: Stokes' Law applies only under laminar flow conditions.
Misinterpreting the Diameter for the Radius: Using the radius instead of the diameter in the equation.
Overlooking the Effect of Temperature: The medium's viscosity can change with temperature, altering the terminal velocity.
Assuming Density is Constant: The densities of the particle and medium can vary with temperature and pressure.

Frequently Asked Questions

What happens if the flow is not laminar?
Stokes' Law applies to laminar flow conditions. Other models should be used for turbulent flow.
Can we use Stokes' Law for non-spherical particles?
Stokes' Law is derived for spherical particles. For non-spherical particles, corrections are necessary.
How does temperature affect terminal velocity?
Temperature can change the viscosity of the fluid, affecting the terminal velocity.
Why is particle density critical in calculating terminal velocity?
The density difference between the particle and the medium influences the gravitational force acting on the particle.
Can terminal velocity vary within the same medium?
Yes, factors like particle size, shape, density, and medium viscosity can cause variations.