Froude Number Equations Formulas Calculator
Open Channel Flow Fluid Mechanics Hydraulics
Problem:
Solve for area of section flow.
Enter Calculator Inputs:
Can you share this page? Because, it could help others.
Solution:
Solution In Other Units:
Input Unit Conversions:
Change Equation or Formulas:
Tap or click to solve for a different unknown or equation
| hydraulic radius | |
| area of section flow | |
| wetted perimeter | |
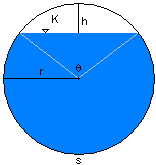 | hydraulic radius of a pipe |
| mean depth | |
| area of section flow | |
| top water surface width |
| Froude number | |
| flow velocity | |
| acceleration of gravity | |
| mean depth |
Froude Number: Significance in Fluid Mechanics
The Froude number, named after the British engineer William Froude, is a dimensionless parameter used in fluid mechanics to characterize the flow regime of a fluid to its wave properties. It is crucial in various fields, including naval architecture, river engineering, and hydraulics.
Definition and Calculation
The Froude number (Fr) is defined as the ratio of the flow velocity to the wave velocity:
Fr = V / √(g * L)
where:
- Fr is the Froude number
- V is the characteristic flow velocity
- g is the gravitational acceleration
- L is the characteristic length
The characteristic flow velocity (V) can vary depending on the application. For example, the open-channel flow might be the average velocity, whereas in ship design, it could be the ship's speed relative to the surrounding water. The characteristic length (L) represents the length scale of the problem at hand, such as a dam's height or a ship's length.
Flow Classification
The Froude number is essential in determining the type of flow regime that a fluid is experiencing. Depending on its value, flow can be classified into three regimes: subcritical flow (Fr < 1), critical flow (Fr = 1), and supercritical flow (Fr > 1).
- Subcritical Flow (Fr < 1): Subcritical flow occurs when the Froude number is less than 1. In this regime, the flow velocity is less than the wave velocity, resulting in smooth, subsonic flow. The flow is typically tranquil and appears to have a stable water surface. Subcritical flow is commonly observed in peaceful rivers, calm hydraulic structures, and low-velocity flow situations.
- Critical Flow (Fr = 1): Critical flow occurs when the Froude number equals 1. In this regime, the flow velocity is approximately equal to the wave velocity, and conditions are balanced. Critical flow is fascinating in the design of hydraulic structures, as it determines the transition from subcritical to supercritical flow.
- Supercritical Flow (Fr > 1): Supercritical flow occurs when the Froude number exceeds 1. In this regime, the flow velocity is greater than the wave velocity. Supercritical flow is characterized by rapid, turbulent flow with violent water surface fluctuations. It is typically observed in steep rivers, rapids, hydraulic jumps, and high-velocity flow situations.
Interpretation and Applications
The Froude number provides valuable insights into various fluid flow phenomena and is widely used in different applications:
- Naval Architecture: The Froude number determines the model scale relative to the full-scale vessel in ship design and maritime engineering. By matching the Froude number between the model and the prototype, engineers can accurately predict the performance and behavior of the full-size ship.
- River Engineering: The Froude number is crucial in the design of river channels, dams, and flood control structures. It helps determine the appropriate flow conditions to prevent channel erosion, control sediment transport, and optimize hydraulic structures' stability.
- Hydraulics: The Froude number guides the analysis and design of open-channel flow. It aids in determining the channel characteristics, such as depth and flow rate, required for efficient and safe hydraulic systems.
- Coastal Engineering: In coastal and offshore engineering, the Froude number is used to assess the impact of waves on structures like breakwaters and jetties. By considering the Froude number, engineers can design structures capable of withstanding wave forces and minimizing coastal erosion.
- River Navigation: The Froude number helps determine the navigability of rivers and channels for ships and boats. By considering the Froude number, waterway authorities can establish the maximum allowable speed for vessel traffic to ensure safe navigation.
Limitations and Considerations
While the Froude number is a valuable parameter in fluid mechanics, it has certain limitations and considerations:
- Sensitivity to Flow Conditions: The Froude number can be susceptible to changes in flow conditions, particularly in the critical flow regime. Slight variations in flow velocity or channel geometry can significantly impact the Froude number and the associated flow regime.
- Incompressible Flow Assumption: The Froude number assumes incompressible flow, which may limit its applicability in specific scenarios involving compressible fluids or high-speed flows.
- Single-Phase Flow: The Froude number is typically used for single-phase flows, such as liquid flow in rivers and channels. Without appropriate modifications, It may not apply directly to multiphase flow situations, such as gas-liquid or solid-liquid flows.
- Boundary Effects: The Froude number does not account for boundary effects like wall friction or channel roughness. These effects can significantly influence the flow behavior but are not explicitly captured in the Froude number calculation.
Practical Examples
To illustrate the practical applications of the Froude number, here are a few examples:
- Determining the suitable model scale for testing ship designs in a wave tank, ensuring accurate predictions of full-scale performance.
- Designing channel transitions and hydraulic jumps in open-channel flow systems to maintain safe and efficient flow conditions.
- Analyzing the stability and efficiency of a spillway in a dam to prevent erosion and control the flow discharge.
- Assessing the impact of coastal waves on the stability of breakwaters and coastal protection structures.
- Determining the maximum allowed speed of a vessel in a river or canal ensures safe navigation and prevents damage to the ship or surrounding structures.
The Froude number is a dimensionless parameter with significant implications in fluid mechanics. It aids in classifying flow regimes, guiding design decisions, predicting flow behavior, and optimizing performance in various fields. By considering the Froude number, engineers and scientists can gain valuable insights into fluids' wave properties and flow characteristics, enabling safer and more efficient designs of hydraulic systems, naval architectures, and river engineering projects.
Online Web Apps, Rich Internet Application, Technical Tools, Specifications, How to Guides, Training, Applications, Examples, Tutorials, Reviews, Answers, Test Review Resources, Analysis, Homework Solutions, Worksheets, Help, Data and Information for Engineers, Technicians, Teachers, Tutors, Researchers, K-12 Education, College and High School Students, Science Fair Projects and Scientists
By Jimmy Raymond
![]()
Contact: aj@ajdesigner.com
Privacy Policy, Disclaimer and Terms
Copyright 2002-2015