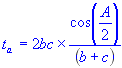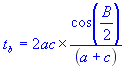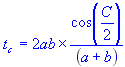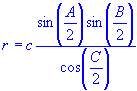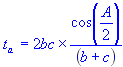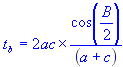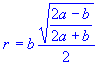Triangle Equations Formulas Calculator
Mathematics - Geometry
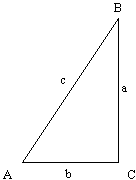
Right Triangle
Problem:
Solve for angle bisector of side c:
Enter Calculator Inputs:
Can you share this page? Because, it could help others.
Solution:
Enter input values and press Calculate.
Solution In Other Units:
Enter input values and press Calculate.
Input Unit Conversions:
Enter input values and press Calculate.
Change Equation or Formulas:
Tap or click to solve for a different unknown or equation
Scalene Triangle:
No sides have equal length
No angles are equal
No sides have equal length
No angles are equal
Scalene Triangle Equations
These equations apply to any type of triangle. Reduced
equations for equilateral, right and isosceles are below.
These equations apply to any type of triangle. Reduced
equations for equilateral, right and isosceles are below.
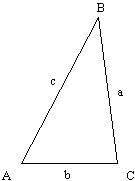
Law of Cosines
| length of side a | |
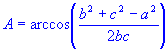 | angle of A |
Equilateral Triangle:
All three sides have equal length
All three angles are equal to 60 degrees
All three sides have equal length
All three angles are equal to 60 degrees
Equilateral Triangle Equations
| Perimeter | |
| Semiperimeter | |
| Area | |
| Altitude | |
| Median | |
| Angle Bisector | |
| Circumscribed Circle Radius | |
| Inscribed Circle Radius |

Right Triangle:
One angle is equal to 90 degrees
One angle is equal to 90 degrees
Right Triangle Equations
Isosceles Triangle:
Two sides have equal length
Two angles are equal
Two sides have equal length
Two angles are equal
Isosceles Triangle Equations
Where
| P | = | Perimeter |
| s | = | Semiperimeter |
| a | = | Length of side a |
| b | = | Length of side b |
| c | = | Length of side c |
| h | = | Altitude |
| m | = | Median |
| A | = | Angle A |
| B | = | Angle B |
| C | = | Angle C |
| t | = | Angle bisector |
| R | = | Circumscribed Circle Radius |
| r | = | Inscribed Circle Radius |
Reference - Books:
1) Max A. Sobel and Norbert Lerner. 1991. Precalculus Mathematics. Prentice Hall. 4th ed.
Infant Growth Charts - Baby Percentiles
Overtime Pay Rate Calculator
Salary Hourly Pay Converter - Jobs
Percent Off - Sale Discount Calculator
Pay Raise Increase Calculator
Linear Interpolation Calculator
Dog Age Calculator
Heat Index Weather Calculator
Pump Calculator - Water Hydraulics
Math Equations Formulas Calculators
Trigonometry Equations Calculator
Horsepower Car Equations Calculator
Ideal Gas Law Calculator
Paycheck Calculator - Overtime Rate
Einstein Energy Equations Calculator
Real Estate Investment Calculators
Home: PopularIndex 1Index 2Index 3Index 4Infant ChartMath GeometryPhysics ForceFluid MechanicsFinanceLoan CalculatorNursing Math
Online Web Apps, Rich Internet Application, Technical Tools, Specifications, How to Guides, Training, Applications, Examples, Tutorials, Reviews, Answers, Test Review Resources, Analysis, Homework Solutions, Worksheets, Help, Data and Information for Engineers, Technicians, Teachers, Tutors, Researchers, K-12 Education, College and High School Students, Science Fair Projects and Scientists
By Jimmy Raymond
![]()
Contact: aj@ajdesigner.com
Privacy Policy, Disclaimer and Terms
Copyright 2002-2015